What is PageRank?
PageRank is a link analysis algorithm named after both the term “web page” and the co-founder Larry “Page” himself. PageRank has been a game-changer in evaluating the relevance and authority of web pages.
Its fundamental idea is straightforward yet powerful: the importance of a webpage is largely determined by the number and quality of links pointing to it, much like how votes work.
The real beauty of PageRank lies in its recursive nature. Essentially, a webpage gains significance if other reputable pages link to it. It’s helpful to think of this as a random web surfer clicking through links; the chances of them landing on a particular page help determine that page’s rank.
This concept transforms the web into a network of interconnected nodes (webpages), linked by hyperlinks, mirroring how Google uses crawlers to index the web.
PageRank isn’t a one-time calculation but an evolving process. It goes through several rounds of refinements to ensure the rankings it assigns to web pages closely mirror their actual importance. It’s this continuous adaptation that has kept PageRank relevant.
Although the patents related to PageRank expired on September 24, 2019, its principles still significantly influence how Google – and indeed, the broader world – navigates and interprets the vastness of the web.
Here is the to Google’s PageRank Patent (now expired).
History of PageRank
TLDR version of Google’s PageRank History
April 1, 1998: The Anatomy of a Large-Scale Hypertextual Web Search Engine paper was published.
September 1, 1998: PageRank patent filed
September 4, 1998: Google was founded
Detailed Information on the History of Google’s PageRank
The journey of PageRank began at Stanford University in 1996, where Larry Page and Sergey Brin, under the guidance of Professor Héctor García-Molina, embarked on a research project to create a new kind of search engine.
The fundamental idea was revolutionary: rank information on the web by the popularity of links, where a page with more links would rank higher.
The roots of PageRank’s algorithm, however, trace back to concepts developed much earlier. The eigenvalue problem, central to PageRank’s methodology, was first applied in scoring contexts as early as 1895 by Edmund Landau for chess tournaments and later by others in various fields, from scientometrics to cognitive models.
Interestingly, the concept of ranking pages based on link analysis was also independently developed by Robin Li of IDD Information Services in 1996, leading to the creation of the RankDex search engine. Li’s work, acknowledged by Page in his patents, was pivotal in the development of ranking algorithms.
PageRank’s development was marked by significant milestones. The initial prototype and the theoretical foundation of the algorithm were detailed in “The Anatomy of a Large-Scale Hypertextual Web Search Engine,” published by Page and Brin on April 1, 1998.
Following this, Google Inc. was founded on September 4, 1998, soon after the first PageRank patent was filed in September of the same year. This patent was assigned to Stanford University, which, in a landmark deal, granted Google exclusive license rights in exchange for 1.8 million shares.
The legacy of PageRank is enriched by its intellectual heritage. It drew inspiration from Eugene Garfield’s citation analysis from the 1950s and Massimo Marchiori’s Hyper Search. The same year that PageRank was introduced, Jon Kleinberg published his work on HITS, further contributing to the field. These influences underscore the algorithm’s depth and interdisciplinary roots.
Refinement and Evolution of PageRank
Google continued to evolve and refine PageRank over the years. The launch of the Google Toolbar in December 2000 made PageRank scores visible to users, and subsequent patents, like the Reasonable Surfer Model filed in 2004 and the Seed Sets patent of 2006, expanded its complexity.
The retirement of the Google Toolbar in March 2016 marked the end of an era, but PageRank’s influence persists. It remains foundational in how Google assesses the importance of webpages, a testament to its enduring relevance in the ever-evolving domain of search engine technology.
How does PageRank Work and How is PageRank Calculated?
Here’s a simplified explanation of how PageRank is calculated and how it works:
Basic Concept
PageRank operates on the principle that important websites are likely to receive more links from other sites. Each link to a page on your site from another site adds to your site’s PageRank.
Numerical Weighting
PageRank assigns a numerical weight to each element of a hyperlinked set of documents, like the World Wide Web. This weight is an indication of the page’s relative importance within the set.
Recursive Definition
The PageRank of a page is defined recursively and depends on the number and PageRank metric of all pages that link to it. In simpler terms, a page that is linked to by many pages with high PageRank receives a high rank itself.
The Damping Factor
The algorithm includes a damping factor, typically set around 0.85. This factor represents the probability that a person will continue clicking on links. The damping factor adjusts the PageRank by considering the likelihood that a user will start a new search.
Calculation Method
The PageRank value for any page is calculated by summing the PageRank of every page that links to it, divided by the number of links on those pages. This process involves several iterations to refine the PageRank values.
Simplified Example
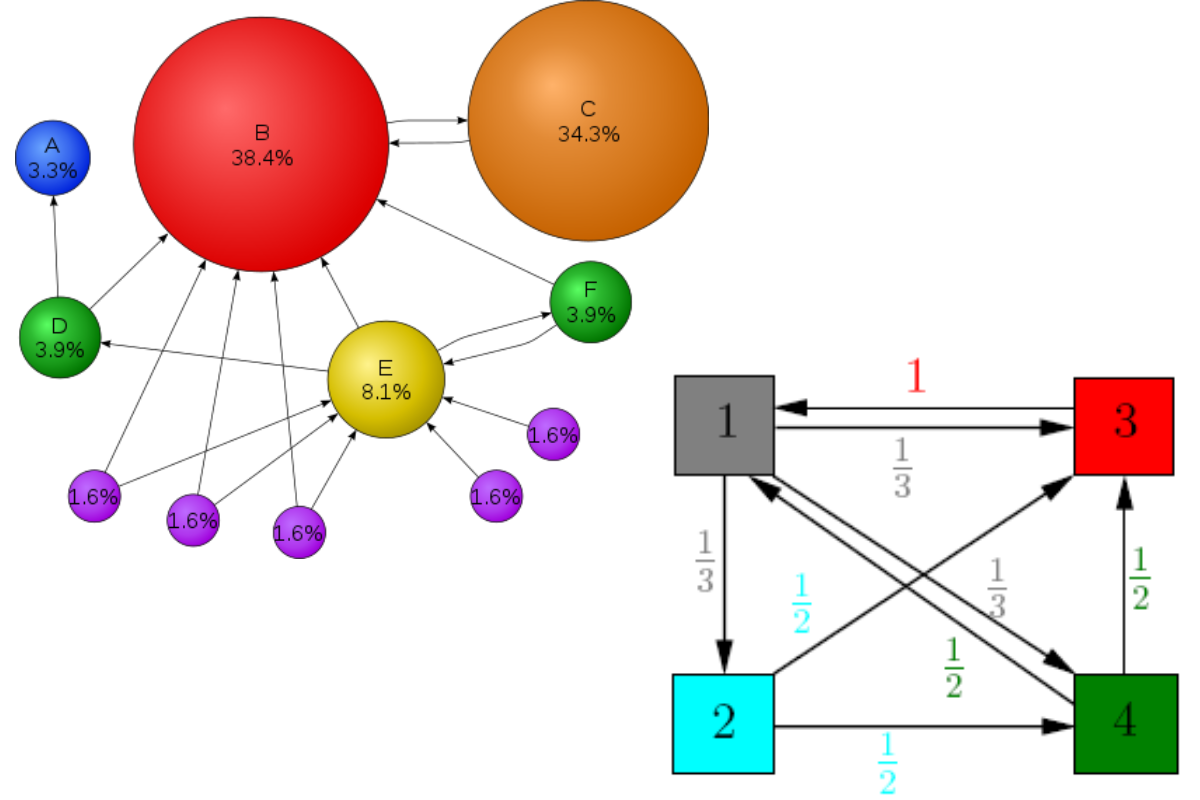
Imagine a small network of four pages (A, B, C, D). If page B has links to A and C, and page C links to A, and D links to all three, the PageRank for A is calculated based on the PageRank of B, C, and D, divided by the number of links they each have.
Random Surfer Model
The algorithm can be thought of as modeling the behavior of a random surfer who is clicking on links at random and switching to a different page occasionally. The PageRank value reflects the chance that the random surfer will land on a particular page.
Iteration and Convergence
The PageRank values are adjusted over several iterations until they converge to a stable value. This iterative process is necessary to accurately reflect the interconnected nature of the web.
PageRank Formula
I have spent countless hours trying to understand the PageRank formula and how it is calculated mathematically.
But rather than explaining the PageRank formula in my own way, I would prefer quoting it straight from the paper The Anatomy of a Large-Scale Hypertextual Web Search Engine where it was mentioned first.
So here it is.
PageRank is defined as follows:
We assume page A has pages T1…Tn which point to it (i.e., are citations). The parameter d is a damping factor which can be set between 0 and 1. We usually set d to 0.85. There are more details about d in the next section. Also C(A) is defined as the number of links going out of page A. The PageRank of a page A is given as follows:
PR(A) = (1-d) + d (PR(T1)/C(T1) + … + PR(Tn)/C(Tn))
PR(A): The PageRank of page A
PR(Tn): The importance of page Tn
C(Tn): The number of links on page Tn
d: A damping factor that represents the chance that a web surfer will stop surfing
Note that the PageRanks form a probability distribution over web pages, so the sum of all web pages’ PageRanks will be one.
PageRank or PR(A) can be calculated using a simple iterative algorithm, and corresponds to the principal eigenvector of the normalized link matrix of the web.
Conclusion
Although the original PageRank patent has expired, it does not mean Google has stopped using PageRank one of the many ranking signals. It surely has evolved into more refined technologies and systems.
But as an SEO, if you haven’t studied about PageRank, are you even an SEO!
Below are some resources I used to study about PageRank. Hope this helps.
- http://infolab.stanford.edu/~backrub/google.html
- https://patents.google.com/patent/US6285999
- https://en.wikipedia.org/wiki/PageRank
- https://pi.math.cornell.edu/~mec/Winter2009/RalucaRemus/Lecture3/lecture3.html
- https://web.stanford.edu/class/cs54n/handouts/24-GooglePageRankAlgorithm.pdf
- https://snap-stanford.github.io/cs224w-notes/network-methods/pagerank
- https://patents.google.com/patent/US9165040B1/en
- https://patents.google.com/patent/US7716225B1/en